All kinds of predictor evaluations are performed using this function.
performance(prediction.obj, measure, x.measure = "cutoff", ...)Arguments
- prediction.obj
An object of class
prediction.- measure
Performance measure to use for the evaluation. A complete list of the performance measures that are available for
measureandx.measureis given in the 'Details' section.- x.measure
A second performance measure. If different from the default, a two-dimensional curve, with
x.measuretaken to be the unit in direction of the x axis, andmeasureto be the unit in direction of the y axis, is created. This curve is parametrized with the cutoff.- ...
Optional arguments (specific to individual performance measures).
Value
An S4 object of class performance.
Details
Here is the list of available performance measures. Let Y and \(\hat{Y}\) be random variables representing the class and the prediction for a randomly drawn sample, respectively. We denote by \(\oplus\) and \(\ominus\) the positive and negative class, respectively. Further, we use the following abbreviations for empirical quantities: P (# positive samples), N (# negative samples), TP (# true positives), TN (# true negatives), FP (# false positives), FN (# false negatives).
acc:Accuracy. \(P(\hat{Y}=Y)\). Estimated as: \(\frac{TP+TN}{P+N}\).
err:Error rate. \(P(\hat{Y}\ne Y)\). Estimated as: \(\frac{FP+FN}{P+N}\).
fpr:False positive rate. \(P(\hat{Y}=\oplus | Y = \ominus)\). Estimated as: \(\frac{FP}{N}\).
fall:Fallout. Same as
fpr.tpr:True positive rate. \(P(\hat{Y}=\oplus|Y=\oplus)\). Estimated as: \(\frac{TP}{P}\).
rec:Recall. Same as
tpr.sens:Sensitivity. Same as
tpr.fnr:False negative rate. \(P(\hat{Y}=\ominus|Y=\oplus)\). Estimated as: \(\frac{FN}{P}\).
miss:Miss. Same as
fnr.tnr:True negative rate. \(P(\hat{Y} = \ominus|Y=\ominus)\).
spec:Specificity. Same as
tnr.ppv:Positive predictive value. \(P(Y=\oplus|\hat{Y}=\oplus)\). Estimated as: \(\frac{TP}{TP+FP}\).
prec:Precision. Same as
ppv.npv:Negative predictive value. \(P(Y=\ominus|\hat{Y}=\ominus)\). Estimated as: \(\frac{TN}{TN+FN}\).
pcfall:Prediction-conditioned fallout. \(P(Y=\ominus|\hat{Y}=\oplus)\). Estimated as: \(\frac{FP}{TP+FP}\).
pcmiss:Prediction-conditioned miss. \(P(Y=\oplus|\hat{Y}=\ominus)\). Estimated as: \(\frac{FN}{TN+FN}\).
rpp:Rate of positive predictions. \(P( \hat{Y} = \oplus)\). Estimated as: (TP+FP)/(TP+FP+TN+FN).
rnp:Rate of negative predictions. \(P( \hat{Y} = \ominus)\). Estimated as: (TN+FN)/(TP+FP+TN+FN).
phi:Phi correlation coefficient. \(\frac{TP \cdot TN - FP \cdot FN}{\sqrt{ (TP+FN) \cdot (TN+FP) \cdot (TP+FP) \cdot (TN+FN)}}\). Yields a number between -1 and 1, with 1 indicating a perfect prediction, 0 indicating a random prediction. Values below 0 indicate a worse than random prediction.
mat:Matthews correlation coefficient. Same as
phi.mi:Mutual information. \(I(\hat{Y},Y) := H(Y) - H(Y|\hat{Y})\), where H is the (conditional) entropy. Entropies are estimated naively (no bias correction).
chisq:Chi square test statistic.
?chisq.testfor details. Note that R might raise a warning if the sample size is too small.odds:Odds ratio. \(\frac{TP \cdot TN}{FN \cdot FP}\). Note that odds ratio produces Inf or NA values for all cutoffs corresponding to FN=0 or FP=0. This can substantially decrease the plotted cutoff region.
lift:Lift value. \(\frac{P(\hat{Y}=\oplus|Y=\oplus)}{P(\hat{Y}=\oplus)}\).
f:Precision-recall F measure (van Rijsbergen, 1979). Weighted harmonic mean of precision (P) and recall (R). \(F = \frac{1}{\alpha \frac{1}{P} + (1-\alpha)\frac{1}{R}}\). If \(\alpha=\frac{1}{2}\), the mean is balanced. A frequent equivalent formulation is \(F = \frac{(\beta^2+1) \cdot P \cdot R}{R + \beta^2 \cdot P}\). In this formulation, the mean is balanced if \(\beta=1\). Currently, ROCR only accepts the alpha version as input (e.g. \(\alpha=0.5\)). If no value for alpha is given, the mean will be balanced by default.
rch:ROC convex hull. A ROC (=
tprvsfpr) curve with concavities (which represent suboptimal choices of cutoff) removed (Fawcett 2001). Since the result is already a parametric performance curve, it cannot be used in combination with other measures.auc:Area under the ROC curve. This is equal to the value of the Wilcoxon-Mann-Whitney test statistic and also the probability that the classifier will score are randomly drawn positive sample higher than a randomly drawn negative sample. Since the output of
aucis cutoff-independent, this measure cannot be combined with other measures into a parametric curve. The partial area under the ROC curve up to a given false positive rate can be calculated by passing the optional parameterfpr.stop=0.5(or any other value between 0 and 1) toperformance.aucpr:Area under the Precision/Recall curve. Since the output of
aucpris cutoff-independent, this measure cannot be combined with other measures into a parametric curve.prbe:Precision-recall break-even point. The cutoff(s) where precision and recall are equal. At this point, positive and negative predictions are made at the same rate as their prevalence in the data. Since the output of
prbeis just a cutoff-independent scalar, this measure cannot be combined with other measures into a parametric curve.cal:Calibration error. The calibration error is the absolute difference between predicted confidence and actual reliability. This error is estimated at all cutoffs by sliding a window across the range of possible cutoffs. The default window size of 100 can be adjusted by passing the optional parameter
window.size=200toperformance. E.g., if for several positive samples the output of the classifier is around 0.75, you might expect from a well-calibrated classifier that the fraction of them which is correctly predicted as positive is also around 0.75. In a well-calibrated classifier, the probabilistic confidence estimates are realistic. Only for use with probabilistic output (i.e. scores between 0 and 1).mxe:Mean cross-entropy. Only for use with probabilistic output. \(MXE :=-\frac{1}{P+N}( \sum_{y_i=\oplus} ln(\hat{y}_i) + \sum_{y_i=\ominus} ln(1-\hat{y}_i))\). Since the output of
mxeis just a cutoff-independent scalar, this measure cannot be combined with other measures into a parametric curve.rmse:Root-mean-squared error. Only for use with numerical class labels. \(RMSE:=\sqrt{\frac{1}{P+N}\sum_i (y_i - \hat{y}_i)^2}\). Since the output of
rmseis just a cutoff-independent scalar, this measure cannot be combined with other measures into a parametric curve.sar:Score combinining performance measures of different characteristics, in the attempt of creating a more "robust" measure (cf. Caruana R., ROCAI2004): SAR = 1/3 * ( Accuracy + Area under the ROC curve + Root mean-squared error ).
ecost:Expected cost. For details on cost curves, cf. Drummond&Holte 2000,2004.
ecosthas an obligatory x axis, the so-called 'probability-cost function'; thus it cannot be combined with other measures. While usingecostone is interested in the lower envelope of a set of lines, it might be instructive to plot the whole set of lines in addition to the lower envelope. An example is given indemo(ROCR).cost:Cost of a classifier when class-conditional misclassification costs are explicitly given. Accepts the optional parameters
cost.fpandcost.fn, by which the costs for false positives and negatives can be adjusted, respectively. By default, both are set to 1.
Note
Here is how to call performance() to create some standard
evaluation plots:
- ROC curves:
measure="tpr", x.measure="fpr".
- Precision/recall graphs:
measure="prec", x.measure="rec".
- Sensitivity/specificity plots:
measure="sens", x.measure="spec".
- Lift charts:
measure="lift", x.measure="rpp".
References
A detailed list of references can be found on the ROCR homepage at https://ipa-tys.github.io/ROCR/.
See also
Examples
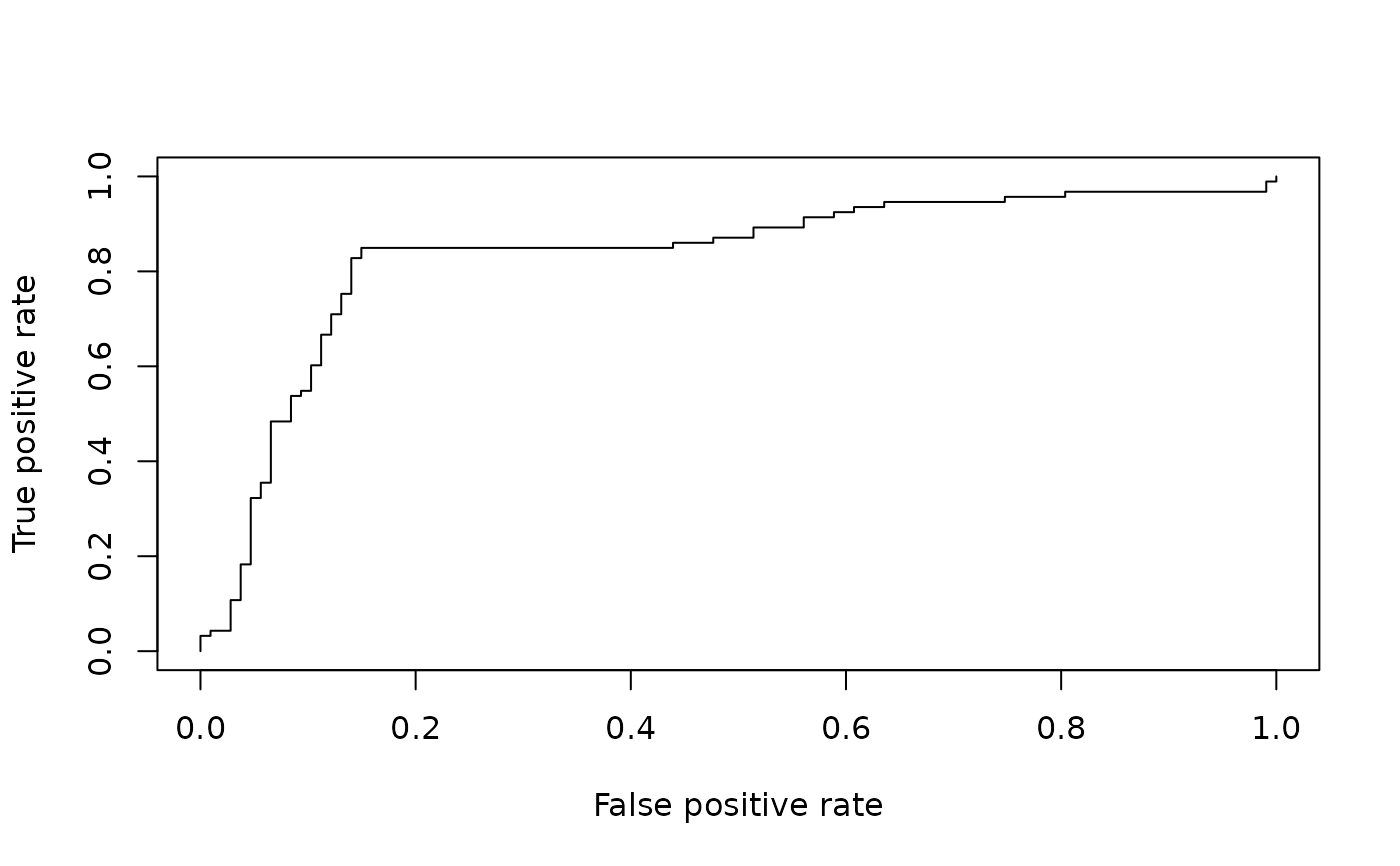
# computing a simple ROC curve (x-axis: fpr, y-axis: tpr)
library(ROCR)
data(ROCR.simple)
pred <- prediction( ROCR.simple$predictions, ROCR.simple$labels)
pred
#> A prediction instance
#> with 200 data points
perf <- performance(pred,"tpr","fpr")
perf
#> A performance instance
#> 'False positive rate' vs. 'True positive rate' (alpha: 'Cutoff')
#> with 201 data points
plot(perf)
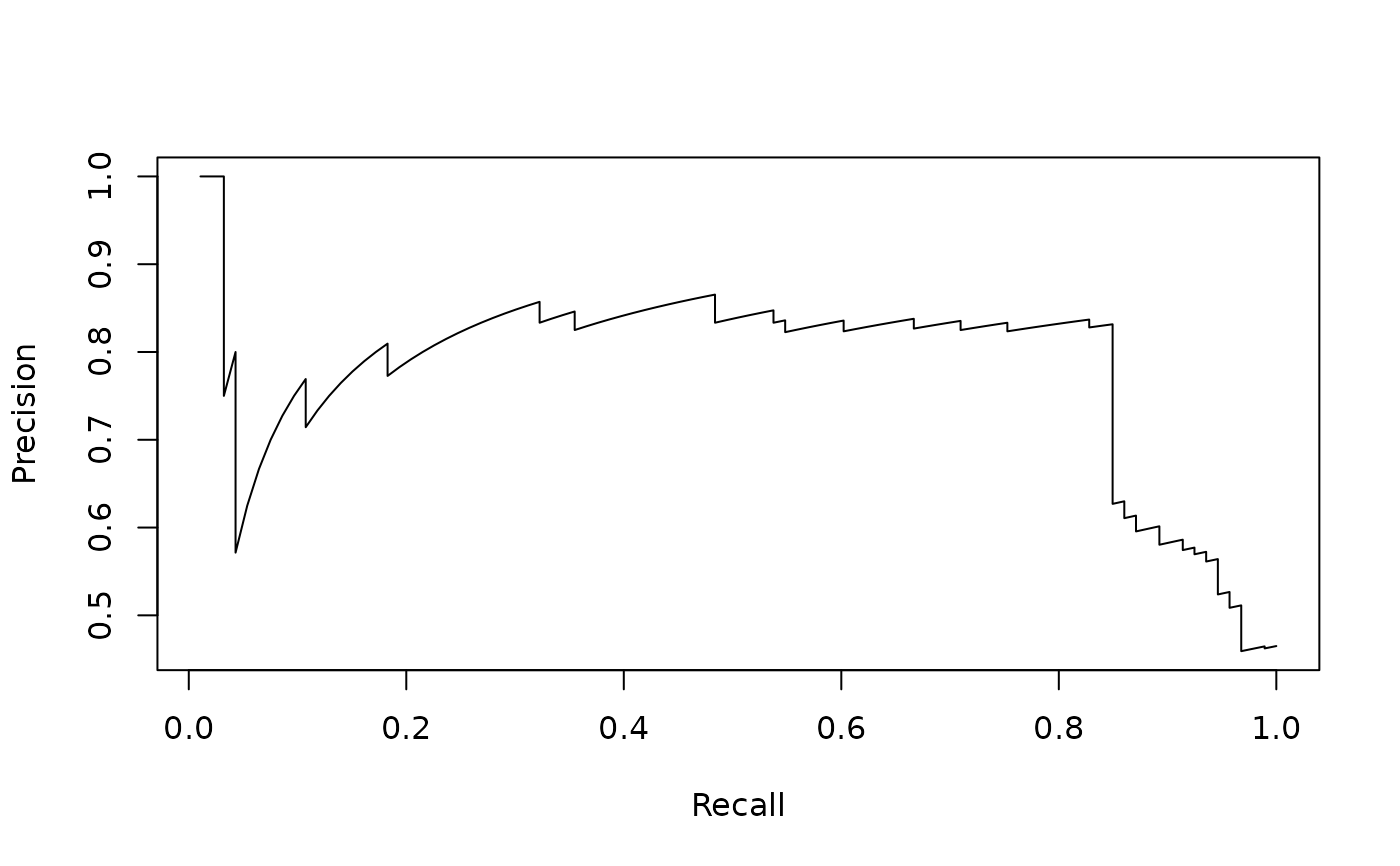
 # precision/recall curve (x-axis: recall, y-axis: precision)
perf <- performance(pred, "prec", "rec")
perf
#> A performance instance
#> 'Recall' vs. 'Precision' (alpha: 'Cutoff')
#> with 201 data points
plot(perf)
# precision/recall curve (x-axis: recall, y-axis: precision)
perf <- performance(pred, "prec", "rec")
perf
#> A performance instance
#> 'Recall' vs. 'Precision' (alpha: 'Cutoff')
#> with 201 data points
plot(perf)
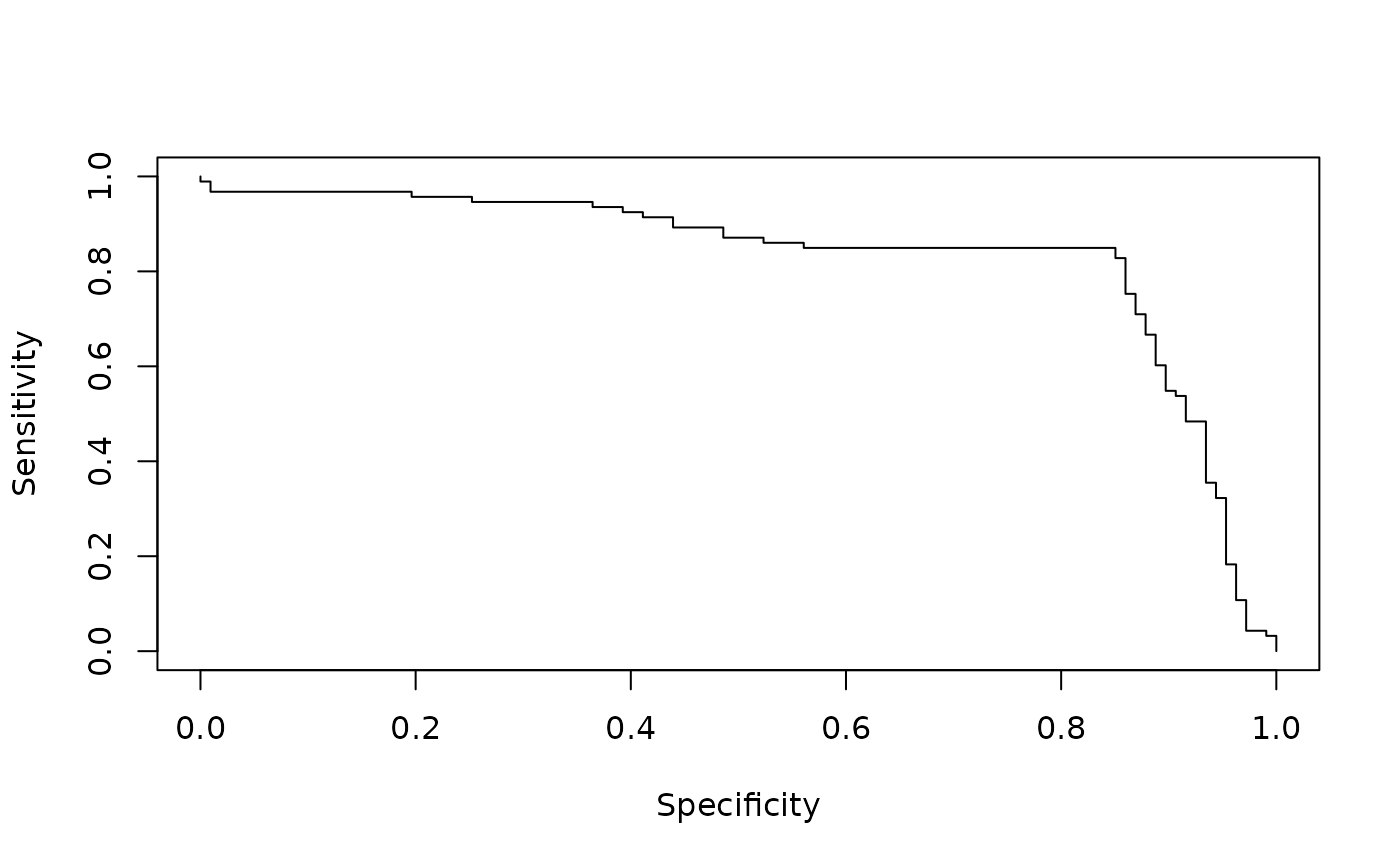
 # sensitivity/specificity curve (x-axis: specificity,
# y-axis: sensitivity)
perf <- performance(pred, "sens", "spec")
perf
#> A performance instance
#> 'Specificity' vs. 'Sensitivity' (alpha: 'Cutoff')
#> with 201 data points
plot(perf)
# sensitivity/specificity curve (x-axis: specificity,
# y-axis: sensitivity)
perf <- performance(pred, "sens", "spec")
perf
#> A performance instance
#> 'Specificity' vs. 'Sensitivity' (alpha: 'Cutoff')
#> with 201 data points
plot(perf)